25373번: 벼락치기
부산사이버대학교에 다니는 대희는 강의 영상 보는 것을 매일 미뤘다. 오늘은 중간고사가 일주일 남은 날이다. 대희는 더 이상 미루면 큰일이 날 것 같아서 오늘부터 밀린 영상을 보기로 했다.
www.acmicpc.net
문제
부산사이버대학교에 다니는 대희는 강의 영상 보는 것을 매일 미뤘다. 오늘은 중간고사가 일주일 남은 날이다. 대희는 더 이상 미루면 큰일이 날 것 같아서 오늘부터 밀린 영상을 보기로 했다. 그런데 아직 정신을 못 차린 대희는 영상을 본 다음 날은 그 전날보다 영상을 적게 본다. 이때 영상을 모두 듣기 위해 첫날 들어야 하는 영상의 개수 중 가장 작은 값을 출력하자.
영상을 하나도 보지 않은 날부터는 계속 영상을 보지 않는 것에 유의하자.
입력
밀린 영상 개수 $N$이 주어진다.
출력
첫날 봐야 하는 영상의 개수 중 가장 작은 값을 출력한다.
제한
$1 \leq N \leq 10^{17}$
예제
| 예제 입력1 | 예제 출력1 |
| 28 | 7 |
| 날짜 | 1일 | 2일 | 3일 | 4일 | 5일 | 6일 | 7일 |
| 영상 개수 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
첫 날에 7개를 들으면 $7 + 6 + \cdots + 2 + 1$로 영상 28개를 정확하게 다 볼 수 있다.
설명
위의 예제를 설명의 예로 들어보자.
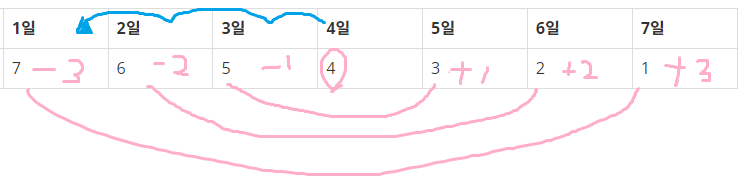
1일엔 7개를 보았고, 7일엔 1개를 보았다. 이 둘을 더해 둘로 나누면, 즉, 서로 양을 나눠가지면 각각 4가 된다. 둘째 날엔 6개를 보았고, 엿새엔 2개를 보았다. 이 역시 마찬가지로 둘을 더해 동일하게 나누면, 각각 4가 된다. 이 방법을 계속하면, 모든 날짜가 동일하게 4를 가질 수 있다. 쉽게 말해, N이 7의 배수라면 N을 7로 나눈 값(평균)이 4일에 해당하는 셈이고, 여기에 3을 더하면 첫째 날에 봐야 할 영상 개수를 알 수 있는 것이다.
만약 7의 배수가 아니라는 조건을 건다면(N%7 != 0) 여기 해당하는 N은 7의 배수보다 최대 6보다 크거나 최소 1보다 클 것이다. 즉, 나머지가 1~6일 것이다. 첫째 날에 봐야 할 강좌 수를 하나 늘리는 것은, 일주일간 들을 수 있는 강좌의 수를 최대 7만큼 늘릴 수 있는 것이므로 나머지를 제한 후, 위 방법으로 첫날 봐야 할 강좌 수를 구한 후 1을 더 해주면 되겠다.
특기할 사항으로는 N이 21 이하인 경우엔 위 공식이 통하지 않는다는 것이다. 따라서 21 이하는 일일이 조건문을 걸어두었다.
코드
n = int(input())
if n <= 1:
print(1)
elif n <= 3:
print(2)
elif n <= 6:
print(3)
elif n <= 10:
print(4)
elif n <= 15:
print(5)
elif n <= 21:
print(6)
elif n%7 == 0:
print(n//7+3)
else:
print(n//7+3+1)
'컴퓨터과학 > Algorithm' 카테고리의 다른 글
| [Python] [백준] 6378번 디지털 루트 (0) | 2022.05.05 |
|---|---|
| [Python] [백준] 1919번 애너그램 만들기 (0) | 2022.04.24 |
| [Python] [백준] 1193번 분수찾기 (0) | 2022.04.24 |