2921번: 도미노
도미노는 여러 종류의 타일 게임에서 사용하는 조각이다. 도미노 조각은 두 칸으로 이루어져 있다. 각 칸에는 점이 찍혀있는데, 점이 안 찍혀져 있을 수도 있다. 점의 개수는 세트의 크기에 의
www.acmicpc.net
문제
도미노는 여러 종류의 타일 게임에서 사용하는 조각이다. 도미노 조각은 두 칸으로 이루어져 있다. 각 칸에는 점이 찍혀있는데, 점이 안 찍혀져 있을 수도 있다. 점의 개수는 세트의 크기에 의해서 결정된다. 세트의 크기가 N인 도미노 세트에서 점의 개수는 0보다 크거나 같고, N보다 작거나 같다. 두 도미노에 찍혀잇는 점의 개수가 같다면, 두 도미노는 동일한 것이다. 예를 들어, 점이 2개와 8개 찍혀있는 도미노는 8개와 2개 찍혀있는 도미노와 같은 도미노이다.
크기가 N인 도미노 세트는 N 또는 그보다 작거나 같은 점을 포함하는 가능한 도미노를 모두 포함하고 있고, 각 도미노는 중복되지 않는다. 다음은 크기가 2인 도미노 세트이다.
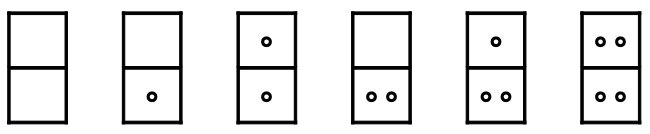
N을 입력받은 뒤, 크기가 N인 도미노 세트에는 점이 몇 개 찍혀 있는지 구하는 프로그램을 작성하시오.
예제
| 예제 입력1 | 예제 출력1 |
| 2 | 12 |
| 예제 입력2 | 예제 출력2 |
| 3 | 30 |
| 예제 입력3 | 예제 출력3 |
| 15 | 2040 |
코드
n = int(input())
res = 0
for i in range(1, n+1):
res += 1.5*i*(i+1)
print(int(res))
설명
두 가지 규칙을 알면 풀 수 있다.
먼저 도미노 상단의 규칙을 보자. N번째 도미노의 상단은 0부터 N개의 점이 등장한다.
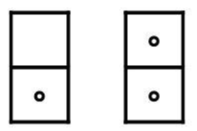
가령 1번째 도미노의 경우, 상단은 점이 0, 1
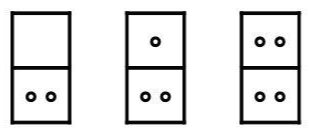
2번째 도미노의 경우, 상단은 점이 0, 1, 2개임을 볼 수 있다.
하단의 규칙은 간단하다. N개의 점이 N+1만큼 등장한다. 가령 1번째 도미노의 경우엔 하단은 1(1+1)개의 점이, 2번째 도미노의 경우엔 하단은 2(2+1)개의 점이 등장한다.
상단의 점 개수는 등차수열로 나타내면 N일 때, $\frac{N(N+1)}{2}$개이고, 하단의 점 개수는 N일 때, $N(N+1)$개다. 즉, N번째 도미노의 점 개수는 이 둘을 더한 $1.5N(N+1)$이다. 0번째의 도미노는 어차피 점의 개수가 0이므로, for문으로 1부터 N+1까지 돌려주면 되겠다.
'컴퓨터과학 > Algorithm' 카테고리의 다른 글
| [Python] [백준] 2669번 직사각형 네개의 합집합의 면적 구하기 (0) | 2022.03.04 |
|---|---|
| [Python] [백준] 13015번 별 찍기 - 23 (0) | 2022.02.27 |
| [R] [Codewars] 8Kyu - Filter out the geese (0) | 2022.01.07 |